Análise
de Sistemas Dinâmicos - Exercícios
Prof.
Alberto Adade Filho (ITA/CTA)
![]() Determinar a série de Fourier para o
trem de impulsos,
Determinar a série de Fourier para o
trem de impulsos,
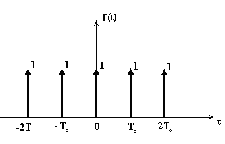
e plotar o espectro de freqüência.
![]() O chamado filtro passa-baixa ideal é aquele que apresenta a
seguinte função do sistema:
O chamado filtro passa-baixa ideal é aquele que apresenta a
seguinte função do sistema:
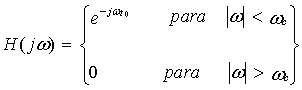
onde wc
é chamada de freqüência de corte do
filtro.
(b) Determinar
e plotar a resposta a impulso do filtro;
![]() Para o sistema abaixo, determinar a
resposta em freqüência senoidal H(jw)
e esboçar os respectivos diagramas de Bode (magnitude e fase):
Para o sistema abaixo, determinar a
resposta em freqüência senoidal H(jw)
e esboçar os respectivos diagramas de Bode (magnitude e fase):

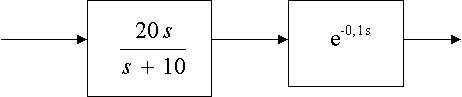
![]() Esboce os diagramas de Bode (magnitude e fase) do
sistema representado pelos blocos abaixo:
Esboce os diagramas de Bode (magnitude e fase) do
sistema representado pelos blocos abaixo:
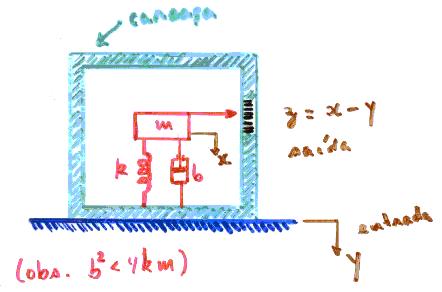
![]() Um modelo físico de um acelerômetro sísmico está ilustrado na figura abaixo. A função de transferência é dada por,
Um modelo físico de um acelerômetro sísmico está ilustrado na figura abaixo. A função de transferência é dada por,
Dado que a freqüência de ressonância do sensor é ![]() rad/s,
rad/s,
![]() A figura abaixo ilustra a representação assintótica
da resposta em freqüência (magnitude em decibéis) de um sistema linear,
invariante no tempo, de fase mínima. Estimar a função transferência deste
sistema.
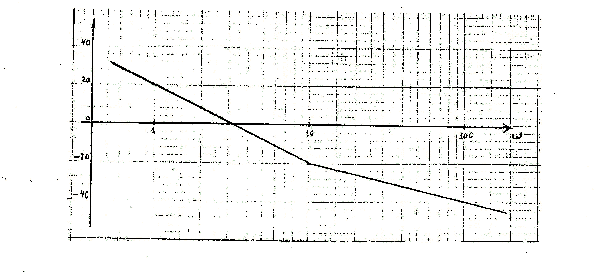
A figura abaixo ilustra a representação assintótica
da resposta em freqüência (magnitude em decibéis) de um sistema linear,
invariante no tempo, de fase mínima. Estimar a função transferência deste
sistema.
![]() A resposta em freqüência de um sistema
eletrohidráulico linear, invariante no tempo, foi obtida conforme os diagramas
de Bode abaixo. Estimar a função de transferência do sistema, G(s).
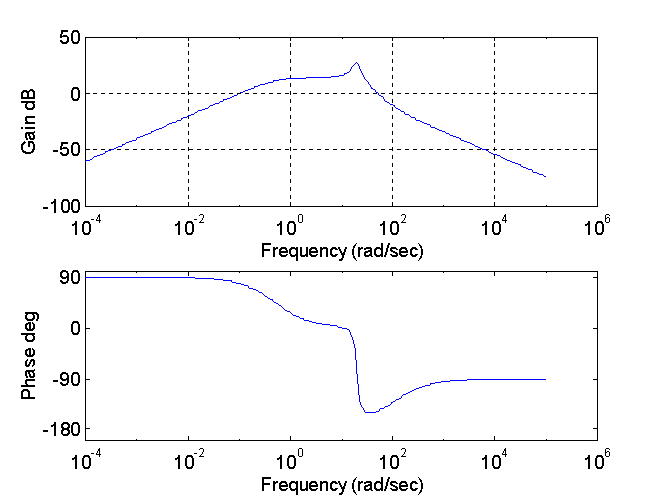
A resposta em freqüência de um sistema
eletrohidráulico linear, invariante no tempo, foi obtida conforme os diagramas
de Bode abaixo. Estimar a função de transferência do sistema, G(s).
![]() A
resposta em freqüência de um sistema linear, invariante no tempo, foi obtida
conforme o diagrama de Bode abaixo. Estimar a função de transferência do
sistema, G(s).
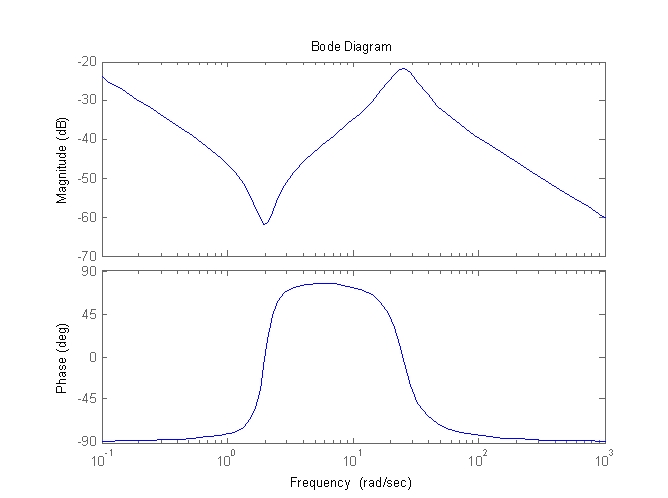
A
resposta em freqüência de um sistema linear, invariante no tempo, foi obtida
conforme o diagrama de Bode abaixo. Estimar a função de transferência do
sistema, G(s).
![]() O motor elétrico de acionamento de um sistema mecânico
possui massa de 20 kg e deve ser instalado sobre quatro absorvedores de
vibração, conforme ilustrado na figura abaixo.
O motor elétrico de acionamento de um sistema mecânico
possui massa de 20 kg e deve ser instalado sobre quatro absorvedores de
vibração, conforme ilustrado na figura abaixo.
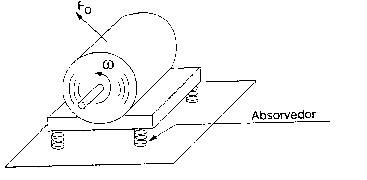
Esse motor deve operar na faixa de 10 a 100 rad/s, e seu rotor possui um desbalanceamento representado pela força F0 = 0,05 w 2, onde F0 é expressa em newtons e w é a rotação do motor em rad/s. Considere os três tipos de absorvedores apresentados na Tabela, despreze qualquer efeito dissipativo e admita apenas o movimento vibratório na direção vertical.
Especifique (justificando) o(s) tipo(s) de absorvedor(es) que deveria(m) ser utilizado(s) para atender a requisitos de montagem que limitam em 1,0 mm o deslocamento vibratório vertical máximo do motor.
Dados/Informações Adicionais
Tabela
Constantes Elásticas dos absorvedores de vibrações
|
Tipo de Absorvedor |
Constante Elástica de cada absorvedor |
|
A |
200000 N/m |
|
B |
20000 N/m |
|
C |
500 N/m |
Amplitude do movimento para vibrações forçadas:
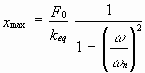
onde keq é a rigidez equivalente do conjunto de absorvedores, e w n é a freqüência natural do sistema.
![]() Para evitar problemas no
funcionamento de um equipamento, cuja massa é de 10 kg, deseja-se limitar a
amplitude das velocidades a que ele será submetido devido a vibrações em
serviço. Testes indicam que acima de 100 Hz a base rígida sobre a qual ele vai
ser montado experimenta as oscilações de maiores amplitudes, e que devem,
portanto, ser minimizadas. Observa-se ainda que a amplitude destes deslocamentos
varia muito pouco nesta faixa de freqüências.
Para evitar problemas no
funcionamento de um equipamento, cuja massa é de 10 kg, deseja-se limitar a
amplitude das velocidades a que ele será submetido devido a vibrações em
serviço. Testes indicam que acima de 100 Hz a base rígida sobre a qual ele vai
ser montado experimenta as oscilações de maiores amplitudes, e que devem,
portanto, ser minimizadas. Observa-se ainda que a amplitude destes deslocamentos
varia muito pouco nesta faixa de freqüências.
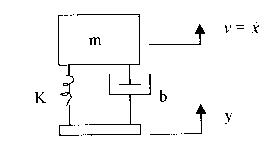
Um engenheiro é incumbido de projetar a fixação do equipamento sobre a base rígida e decide modelar o conjunto equipamento/sistema de fixação como um oscilador linear com um único grau de liberdade. A razão entre as amplitudes da velocidade da massa de um oscilador linear e do deslocamento da base sobre a qual ele está montado varia com a freqüência de acordo com a expressão:
![]()
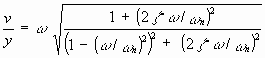
onde v representa a amplitude da velocidade, y a amplitude do deslocamento da base, w (rad/s) a freqüência de oscilação da base, w n a freqüência natural de vibração do oscilador e z a razão de amortecimento do sistema, relacionado com a constante de amortecimento, b, através da equação:
![]()
onde m é a massa do oscilador.
|
SISTEMA DE FIXAÇÃO |
Keq (N/m) |
beq (N s/m) |
|
Sistema A |
4000 |
40 |
|
Sistema B |
4000 |
20 |
|
Sistema C |
16000 |
80 |
![]()
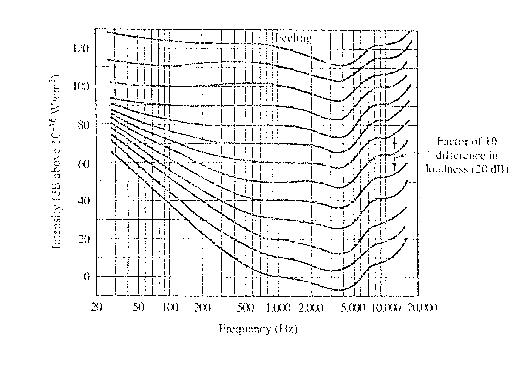
![]() Curvas de nível de mesma intensidade ("loudness")
para o ouvido humano estão mostradas na figura abaixo. Para que um tom de 100
Hz seja percebido na mesma altura ("loudness") que um tom de
1000 Hz, o tom de 100 Hz deve ser aproximadamente 30 dB mais fraco em 100 Hz do
que em 1000 Hz. Achar uma função de transferência que essencialmente tenha a
mesma resposta em freqüência que a terceira curva a partir de baixo do
gráfico.
Curvas de nível de mesma intensidade ("loudness")
para o ouvido humano estão mostradas na figura abaixo. Para que um tom de 100
Hz seja percebido na mesma altura ("loudness") que um tom de
1000 Hz, o tom de 100 Hz deve ser aproximadamente 30 dB mais fraco em 100 Hz do
que em 1000 Hz. Achar uma função de transferência que essencialmente tenha a
mesma resposta em freqüência que a terceira curva a partir de baixo do
gráfico.
![]()